Advertisements
Advertisements
प्रश्न
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
उत्तर
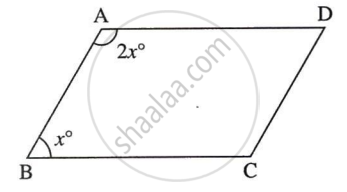
Let `square`ABCD be the parallelogram.
The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.
Let the common multiple be x.
∴ ∠A = x° and ∠B = 2x°
∠A + ∠B = 180° ...[Adjacent angles of a parallelogram are supplementary]
∴ x + 2x = 180
∴ 3x = 180
∴ x = `180/3`
∴ x = 60
∠A = x° = 60°
∠B = 2x°
= 2 × 60° = 120°
∠A = ∠C = 60°
∠B = ∠D= 120° ...[Opposite angles of a parallelogram]
APPEARS IN
संबंधित प्रश्न
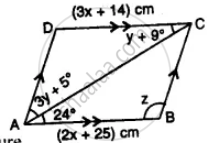
Consider the given parallelogram. Find the values of the unknowns x, y, z.

Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
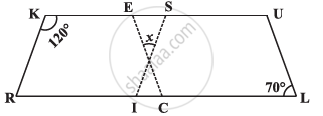
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
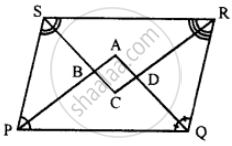
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
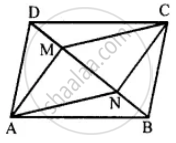
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Use the information given in the alongside diagram to find the value of x, y, and z.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
