Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
उत्तर
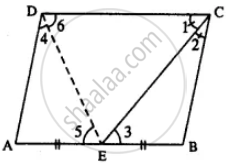
Given: parallelogram ABCD in which E is mid-point of AB and CE bisects ZBCD.
To Prove :
(i) AE = AD
(ii) DE bisects ∠ADC
(iii) ∠DEC = 90°
Const. Join DE
Proof : (i) AB || CD (Given)
and CE bisects it.
∠1 = ∠3 (alternate ∠s) ……… (i)
But ∠1 = ∠2 (Given) …………. (ii)
From (i) & (ii)
∠2 = ∠3
BC = BE (sides opp. to equal angles)
But BC = AD (opp. sides of ||gm)
and BE = AE (Given)
AD = AE
∠4 = ∠5 (∠s opp. to equal sides)
But ∠5 = ∠6 (alternate ∠s)
=> ∠4 = ∠6
DE bisects ∠ADC.
Now AD || BC
=> ∠D + ∠C = 180°
2∠6+2∠1 = 180°
DE and CE are bisectors.
∠6 + ∠1 = `180^circ/2`
∠6 + ∠1 = 90°
But ∠DEC + ∠6 + ∠1 = 180°
∠DEC + 90° = 180°
∠DEC = 180° – 90°
∠DEC = 90°
Hence the result.
APPEARS IN
संबंधित प्रश्न
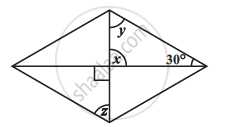
Consider the given parallelograms. Find the values of the unknowns x, y, z.
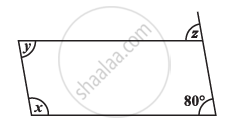
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
