Advertisements
Advertisements
Question
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
Solution
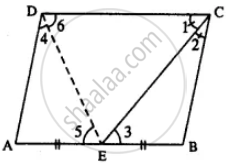
Given: parallelogram ABCD in which E is mid-point of AB and CE bisects ZBCD.
To Prove :
(i) AE = AD
(ii) DE bisects ∠ADC
(iii) ∠DEC = 90°
Const. Join DE
Proof : (i) AB || CD (Given)
and CE bisects it.
∠1 = ∠3 (alternate ∠s) ……… (i)
But ∠1 = ∠2 (Given) …………. (ii)
From (i) & (ii)
∠2 = ∠3
BC = BE (sides opp. to equal angles)
But BC = AD (opp. sides of ||gm)
and BE = AE (Given)
AD = AE
∠4 = ∠5 (∠s opp. to equal sides)
But ∠5 = ∠6 (alternate ∠s)
=> ∠4 = ∠6
DE bisects ∠ADC.
Now AD || BC
=> ∠D + ∠C = 180°
2∠6+2∠1 = 180°
DE and CE are bisectors.
∠6 + ∠1 = `180^circ/2`
∠6 + ∠1 = 90°
But ∠DEC + ∠6 + ∠1 = 180°
∠DEC + 90° = 180°
∠DEC = 180° – 90°
∠DEC = 90°
Hence the result.
APPEARS IN
RELATED QUESTIONS
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
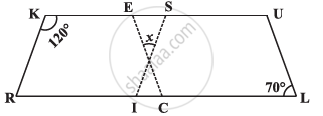
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Name the quadrilaterals whose diagonals bisect each other
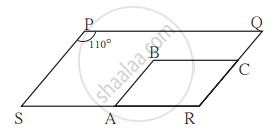
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
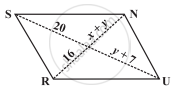
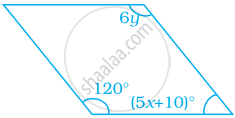
Find the values of x and y in the following parallelogram.
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
The following figure RUNS is parallelogram. Find x and y. (Lengths are in cm)