Advertisements
Advertisements
Question
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
Solution
Given, ABCD is a parallelogram,
So, ∠A = ∠C ...[∵ Opposite angles of a parallelogram are equal]
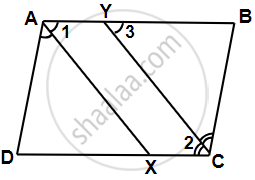
∴ `(∠A)/2 = (∠C)/2` ...[Dividing both the sides by 2]
∠1 = ∠2 ...[Alternative angles]
But ∠2 = ∠3 ...[∵ AB || CD and CY is the transerval]
∴ ∠1 = ∠3
But they are pair of corresponding angles.
∴ AX || YC ...(i)
AY || XC [∵ AB || DC] ...(ii)
From equations (i) and (ii), we get
AXCY is a parallelogram.
APPEARS IN
RELATED QUESTIONS
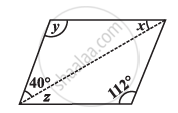
Consider the given parallelogram. Find the values of the unknowns x, y, z.

Consider the given parallelograms. Find the values of the unknowns x, y, z.
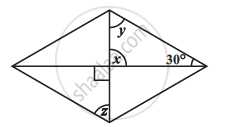
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
ABCD is a parallelogram. Find the value of x, y and z.

Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
