Advertisements
Advertisements
Question
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
Solution
Given, l || m
Now, ∠DXY = ∠XYA ...[Alternate interior angles]
⇒ `(∠DXY)/2 = (∠XYA)/2` ...[Dividing both the sides by 2]
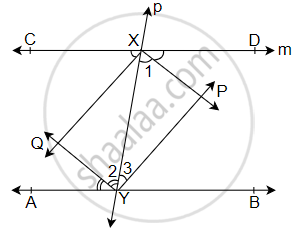
Now, ∠1 = ∠2 ...[Alternate angle are equal]
XP and YQ are bisectors.
So, XP || QY ...(i)
Similarly, XQ || PY ...(ii)
Now, from equation (i) and (ii), we get
In parallelogram PXQY,
∠DXY + ∠XYB = 180° ...(iii) [Interior angles on the same side of transversal are supplementary]
Now, dividing both the sides by 2, get
`(∠DXY)/2 + (∠XYB)/2 = 180^circ/2`
So, ∠1 + ∠3 = 90° [Dividing both the sides by 2] ...(iv)
In triangle XYP,
∠1 + ∠3 + ∠P = 180°
90° + ∠P = 180° ...[From equation (iv)]
∠P = 180° – 90°
∠P = 90° ...(v)
From equations (iii) and (v),
PXQY is a rectangle.
APPEARS IN
RELATED QUESTIONS
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement is true for a rectangle?
All rectangles are squares.
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
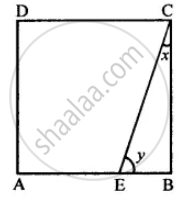
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Every trapezium is a rectangle.
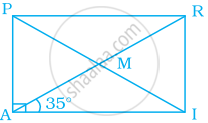
In rectangle PAIR, find ∠ARI, ∠RMI and ∠PMA.
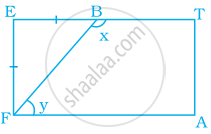
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.