Advertisements
Advertisements
Question
ABCD is a trapezium such that AB || CD, ∠A : ∠D = 2 : 1, ∠B : ∠C = 7 : 5. Find the angles of the trapezium.
Solution
Let ABCD is a trapezium and AB || CD.
Also, angles A and D be 2x and x respectively.
So, 2x + x = 180° ...[In trapezium, the angles on either side of the base are supplementary]
⇒ 3x = 180°
⇒ x = 60°
So, ∠A = 2 × 60° = 120°
And ∠D = 60°
Again, let the angles B and C be 7x and 5x respectively.
So, 7x + 5x = 180°
⇒ 12x = 180°
⇒ x = 15°
Hence, ∠B = 7 × 15 = 105° and ∠C = 5 × 15 = 75°.
APPEARS IN
RELATED QUESTIONS
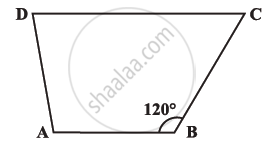
Find m∠C in the following figure if `bar(AB) || bar(DC)`
In `square` IJKL, side IJ || side KL, ∠I = 108°, ∠K = 53° then find the measure of ∠J and ∠L.
In `square`ABCD, side BC < side AD in following figure. side BC || side AD and if side BA ≅ side CD then prove that ∠ABC ≅ ∠DCB.

Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
A quadrilateral in which a pair of opposite sides is parallel is ______.
In trapezium ABCD with AB || CD, if ∠A = 100°, then ∠D = ______.
All angles of a trapezium are equal.
Every trapezium is a parallelogram.
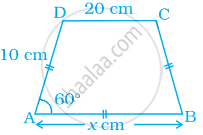
Find the value of x in the trapezium ABCD given below.
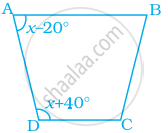
In the following figure, AB || DC and AD = BC. Find the value of x.