Advertisements
Advertisements
Question
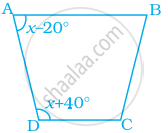
Find the value of x in the trapezium ABCD given below.
Solution
Given, A trapezium ABCD in which ∠A = (x – 20)°, ∠D = (x + 40)°
Since, In a trapezium, the angle on either side of the base are supplementary,
Therefore, (x – 20)° + (x + 40)° = 180°
⇒ x – 20° + x + 40° = 180°
⇒ 2x + 20° = 180°
⇒ 2x = (180° – 20°)
⇒ 2x = 160°
⇒ x = 80°
APPEARS IN
RELATED QUESTIONS
All squares are trapeziums.
In `square`ABCD, side BC < side AD in following figure. side BC || side AD and if side BA ≅ side CD then prove that ∠ABC ≅ ∠DCB.

In an Isosceles-trapezium, show that the opposite angles are supplementary.
Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
Which of the following properties describe a trapezium?
Every rhombus is a trapezium.
Of the four quadrilaterals-square, rectangle, rhombus and trapezium-one is somewhat different from the others because of its design. Find it and give justification.
In a quadrilateral HOPE, PS and ES are bisectors of ∠P and ∠E respectively. Give reason.
Construct a trapezium ABCD in which AB || DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
Construct a trapezium ABCD where AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm and CD = 9.6 cm. Measure ∠B and ∠A.
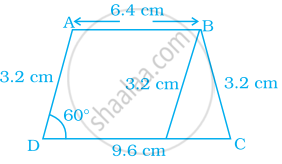
[Hint: Difference of two parallel sides gives an equilateral triangle.]
