Advertisements
Advertisements
Question
Construct a trapezium ABCD in which AB || DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
Solution
We know that,
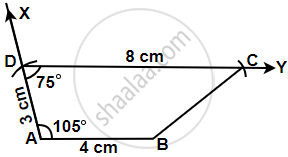
∠A + ∠D = 180° ...[Sum of adjacent angle of a trapezium is 180°]
105° + ∠D = 180°
∠D = 180° – 105°
∠D = 75°
Steps of construction:
Step I: Draw AB = 4 cm.
Step II: Draw `bar(AX)` that is ∠BAX = 105°.
Step III: Mark a point D on AX that is AD = 3 cm.
Step IV: Draw `bar(DY)` that is ∠ADY = 75°.
Step V: Mark a point C that is CD = 8 cm.
Step VI: Join BC.
Hence, ABCD is the required trapezium.
APPEARS IN
RELATED QUESTIONS
All parallelograms are trapeziums.
All squares are trapeziums.
Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
Which of the following figures do not satisfy any of the following properties?
- All sides are equal.
- All angles are right angles.
- Opposite sides are parallel.
PQRS is a trapezium in which PQ || SR and ∠P = 130°, ∠Q = 110°. Then ∠R is equal to ______.
All angles of a trapezium are equal.
Of the four quadrilaterals-square, rectangle, rhombus and trapezium-one is somewhat different from the others because of its design. Find it and give justification.
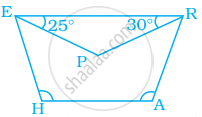
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
ABCD is a trapezium such that AB || CD, ∠A : ∠D = 2 : 1, ∠B : ∠C = 7 : 5. Find the angles of the trapezium.
Construct a trapezium ABCD where AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm and CD = 9.6 cm. Measure ∠B and ∠A.
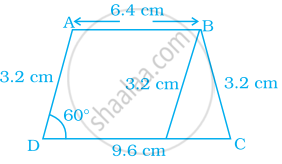
[Hint: Difference of two parallel sides gives an equilateral triangle.]
