Advertisements
Advertisements
Question
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
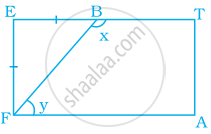
Solution
Given, A rectangle ATEF in which EF = EB.
Then, ΔFEB is an isosceles triangle.
Therefore, by the angle sum property of a triangle, we have
∠EFB + ∠EBF + ∠FEB = 180° ...[Angle sum property of triangle]
⇒ ∠EFB + ∠EBF + 90° = 180° ...[∵ In a rectangle, each angle is of 90°]
⇒ 2∠EFB = 90° ...[∵ ∠EFB = ∠EBF]
∠EFB = 45° and ∠EBF = 45°
Now, ∠x = 180° – 45° = 135° ...[Linear pair]
And ∠EFB + ∠y = 90° ...[∵ In a rectangle, each angle is of 90°]
⇒ ∠y = 90° – 45° = 45°
APPEARS IN
RELATED QUESTIONS
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
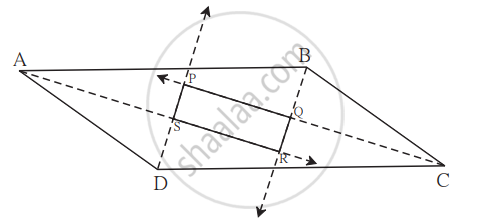
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Show that the bisectors of angles of a parallelogram form a rectangle
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
