Advertisements
Advertisements
प्रश्न
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
उत्तर
As we know that the opposite sides of a parallelogram are equal.
So, AB = DC = 4 cm
BC = AD = 5 cm
∠B = 60°
∠A + ∠B = 180° ...[Sum of cointerior angles]
∠A = 180°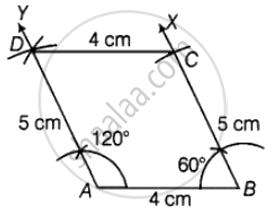
Steps of construction:
Step I: Draw AB = 4 cm.
Step II: Draw ray BX that is ∠ABX = 60°.
Step III: Mark a point C that is BC = 5 cm.
Step IV: Draw a ray AY that is ∠YAB = 120.
Step V: Mark a point D that is AD = 5 cm.
Step VI: Join C and D.
Hence, ABCD is required parallelogram.
APPEARS IN
संबंधित प्रश्न
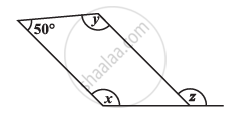
Consider the given parallelogram. Find the values of the unknowns x, y, z.
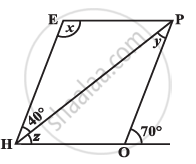
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
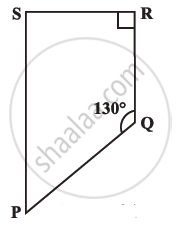
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

Prove that the diagonals of a parallelogram bisect each other.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
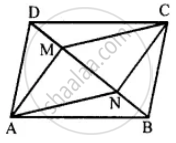
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e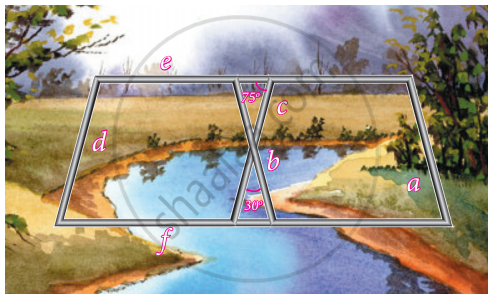
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
