Advertisements
Advertisements
प्रश्न
Prove that the diagonals of a parallelogram bisect each other.
उत्तर

Given: ||gm ABCD in which diagonals AC and BD bisect each other.
To Prove : OA = OC and OB = OD
Proof : AB || CD (Given)
∠1 = ∠2 (alternate ∠s)
∠3 = ∠4 = (alternate ∠s)
and AB = CD (opposite sides of //gm)
∆COD = ∆AOB (A.S.A. rule)
OA = OC and OB = OD
Hence the result.
APPEARS IN
संबंधित प्रश्न
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
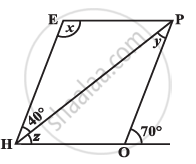
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
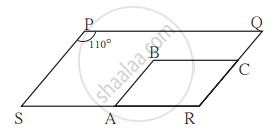
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
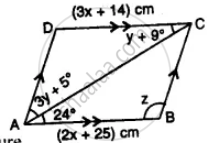
Use the information given in the alongside diagram to find the value of x, y, and z.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between c and f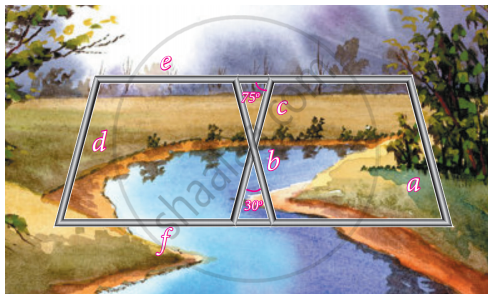
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
