Advertisements
Advertisements
प्रश्न
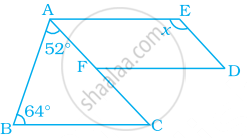
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
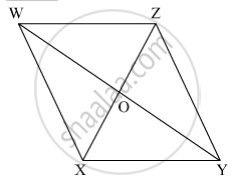
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
उत्तर
WXYZ is a parallelogram.
(1) l(XY) = l(WZ) = 4.5 cm ...(Opposite sides of a parallelogram are congruent)
(2) l(XW) = l(YZ) = 8.2 cm ...(Opposite sides of a parallelogram are congruent)
(3) l(OZ) = l(OX) = 2.5 cm ...(Diagonals of parallelogram bisect each other)
(4) l(WY) = 2 × l(WO) = 2 × 3.3 = 6.6 cm ...(Diagonals of parallelogram bisect each other)
(5) m∠WXY = m∠WZY = 120º ...(Opposite angles of a parallelogram are congruent)
Now,
m∠WZY + m∠XWZ = 180º ...(Adjacent angles of a parallelogram are supplementary)
⇒ 120º + m∠XWZ = 180º
⇒ m∠XWZ = 180º − 120º = 60º
संबंधित प्रश्न
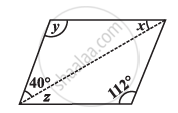
Consider the given parallelograms. Find the values of the unknowns x, y, z.
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
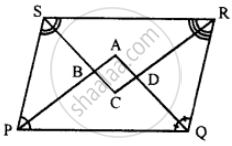
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
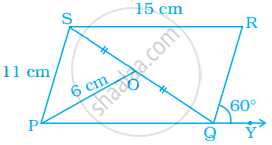
Find the values of x and y in the following parallelogram.
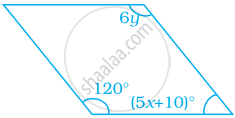
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
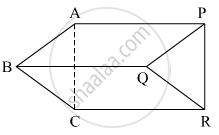
In the following figure, FD || BC || AE and AC || ED. Find the value of x.