Advertisements
Advertisements
प्रश्न
Measures of opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of its each angle.
उत्तर
Let ABCD be the parallelogram.
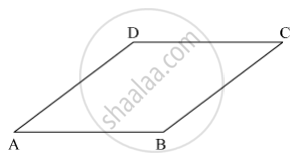
Suppose ∠A = (3x − 2)º and ∠C = (50 − x)º.
We know that the opposite angles of a paralelogram are congruentes.
∴ m∠A = m∠C
⇒ 3x − 2 = 50 − x
⇒ 3x + x = 50 + 2
⇒ 4x = 52
⇒ x = `52/4`
⇒ x = 13
∴ m∠A = (3x − 2)º = (3 × 13 − 2)º = (39 − 2)º = 37º
So, m∠C = m∠A = 37º
Also, the adjacent angles of a parallelogram are supplementary.
∴ m∠A + m∠D = 180º
⇒ 37º + m∠D = 180º
⇒ m∠D = 180º − 37º = 143º
Now,
m∠B = m∠D = 143º (Opposite angles of a parallelogram are congruent)
Thus, the measure of the angles of the parallelogram are 37º, 143º, 37º and 143º.
संबंधित प्रश्न
All rhombuses are kites.
For which of the following figures, diagonals are perpendicular to each other?
Which of the following figures satisfy the following property?
- Has two pairs of congruent adjacent sides.
Which one has all the properties of a kite and a parallelogram?
A quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure is ______.
If only one diagonal of a quadrilateral bisects the other, then the quadrilateral is known as ______.
A kite is not a convex quadrilateral.
Every kite is a parallelogram.
In kite WEAR, ∠WEA = 70° and ∠ARW = 80°. Find the remaining two angles.
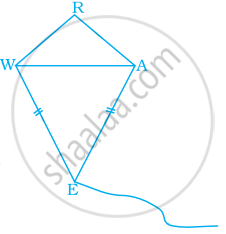
Find the values of x and y in the following kite.