Advertisements
Advertisements
प्रश्न
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
उत्तर
Suppose ABCD is a rectangle.
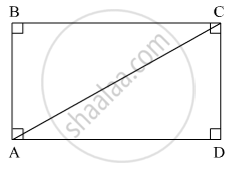
Here, segment AC is a diagonal and segment AD is one side of the rectangle ABCD.
l(AC) = 26 cm and l(AD) = 24 cm.
In right ∆ACD,
l(AC)2 = l(AD)2 + l(CD)2 ...(Pythagoras theorem)
⇒ l(CD)2 = l(AC)2 − l(AD)2
⇒ l(CD)2 = (26)2 − (24)2
⇒ l(CD)2 = 676 − 576 = 100
⇒ l(CD) = `sqrt(100)` = 10 cm
Thus, the other side of the rectangle is 10 cm.
संबंधित प्रश्न
Explain why a rectangle is a convex quadrilateral.
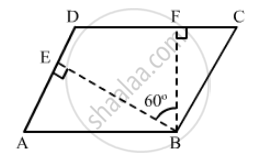
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm then find BO and if ∠CAD =35° then find ∠ACB.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
Rectangle is a regular quadrilateral.
If diagonals of a quadrilateral are equal, it must be a rectangle.
