Advertisements
Advertisements
प्रश्न
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
उत्तर
ABCD is a rhombus.
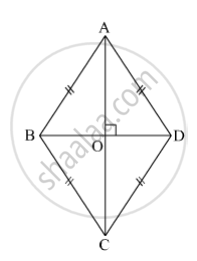
Here, segment AC and segment BD are the diagonals of the rhombus ABCD.
l(AC) = 16 cm and l(BD) = 12 cm.
Diagonals of a rhombus are perpendicular bisectors of each other.
∴ m∠AOD = 90°
Also, l(OA) = `1/2l(AC) = 1/2 xx 16 = 8 cm`
l(OD) = `1/2l(BD) = 1/2`× 12 = 6 cm
In right ∆AOD,
l(AD)2 = l(OA)2 + l(OD)2 ...[Pythagoras theorem]
⇒ l(AD)2 = (8)2 + (6)2
⇒ l(AD)2 = 64 + 36 = 100
⇒ l(AD) = \[\sqrt{100}\] = 10 cm
All sides of a rhombus are equal.
∴ Perimeter of the rhombus ABCD = 4 × Side of a rhombus = 4 × 10 = 40 cm
Thus, the side and perimeter of the rhombus are 10 cm and 40 cm, respectively.
संबंधित प्रश्न
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
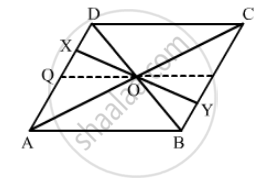
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
All rhombuses are squares.
