Advertisements
Advertisements
Question
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
Solution
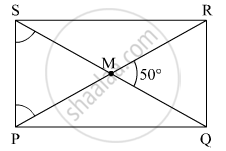
∴ PM =
MS =
Also, PR = QS …(iii) ...(Diagonals of a rectangle are congruent)
∴ PM = MS …(iv) ...[From (i), (ii) and (iii)]
In ∆PMS,
PM = MS ...[From (iv)]
∴ ∠MSP = ∠MPS = x° ...(v) ...(Isosceles triangle theorem)
∠PMS = ∠QMR = 50° ...(vi) ...(Vertically opposite angles)
In ∆MPS,
∠PMS + ∠MPS + ∠MSP = 180° ...(The sum of the measures of the three angles of a triangle is 180°.)
∴ 50° + x + x = 180° ...[From (v) and (vi)]
∴ 50° + 2x = 180°
∴ 2x = 180° - 50°
∴ 2x = 130°
∴ x =
∴ x = 65°
∴ ∠MPS = 65° ...[From (v)]
APPEARS IN
RELATED QUESTIONS
Which of the following statement is true for a rectangle?
It has two pairs of equal sides.
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
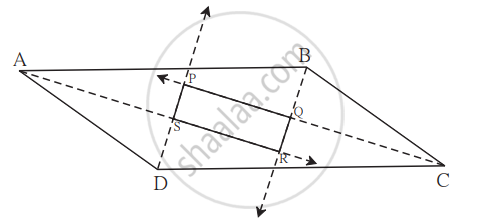
Show that the bisectors of angles of a parallelogram form a rectangle
For which of the following figures, diagonals are equal?
All squares are rectangles.
Rectangle is a regular quadrilateral.
If diagonals of a quadrilateral are equal, it must be a rectangle.
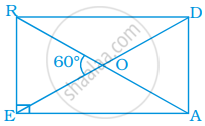
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD