Advertisements
Advertisements
Question
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
Solution
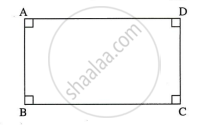
Given: `square`ABCD is a rectangle.
To prove: `square`ABCD is a parallelogram.
Proof:
`square`ABCD is a rectangle.
∠A = ∠B = ∠C = ∠D = 90° ...(angles of rectangle)
∠A = ∠B = ∠C = ∠D ...(each angle 90°)
A quadrilateral is a parallelogram if its pairs of opposite angles are congruent.
∴ `square`ABCD is a parallelogram.
APPEARS IN
RELATED QUESTIONS
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
Which of the following statement is true for a square?
It is a rectangle.
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
A rectangular MORE is shown below:
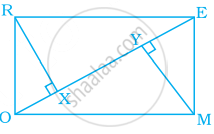
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
