Advertisements
Advertisements
Question
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Solution

\[\text{ Using Pythagoras theorem }: \]
\[A D^2 + D C^2 = A C^2 \]
\[ 5^2 + {12}^2 = A C^2 \]
\[25 + 14 = A C^2 \]
\[169 = A C^2 \]
\[AC = \sqrt{169}\]
\[ = 13 cm\]
\[\text{ Thus, length of the diagonal is 13 cm } .\]
APPEARS IN
RELATED QUESTIONS
Explain why a rectangle is a convex quadrilateral.
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
In the following figure, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
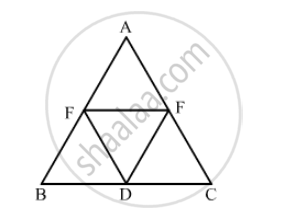
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Which of the following statement is true for a square?
It is a rectangle.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
