Advertisements
Advertisements
प्रश्न
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
उत्तर

\[\text{ Using Pythagoras theorem }: \]
\[A D^2 + D C^2 = A C^2 \]
\[ 5^2 + {12}^2 = A C^2 \]
\[25 + 14 = A C^2 \]
\[169 = A C^2 \]
\[AC = \sqrt{169}\]
\[ = 13 cm\]
\[\text{ Thus, length of the diagonal is 13 cm } .\]
APPEARS IN
संबंधित प्रश्न
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
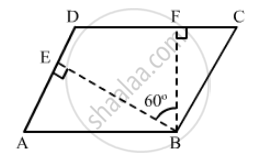
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
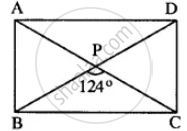
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
Rectangle is a regular quadrilateral.
