Advertisements
Advertisements
Question
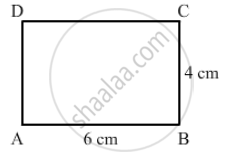
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
Advertisements
Solution
\[\text{ Let the side be x cm and y cm } . \]
\[\text{ So, we have }: \]
\[ 2\left( x + y \right) = 20 \]
\[\text{ Sides are in the ratio 2: 3 } . \]
\[ \therefore y = \frac{3x}{2}\]
\[\text{ Putting the value of y }: \]
\[2\left( x + \frac{3x}{2} \right) = 20 \]
\[\frac{2x + 3x}{2} = 10\]
\[5x = 20\]
\[x = 4\]
\[ \therefore y = \frac{3 \times 4}{2} = 6\]
\[\text{ Thus, sides of the rectangle will be 4 cm and 6 cm } . \]
\[\text{ ABCD is the rectangle having sides 4 cm and 6 cm } .\]
RELATED QUESTIONS
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
All rectangles are squares.
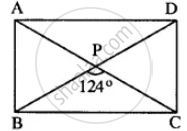
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
A quadrilateral whose opposite sides and all the angles are equal is a ______.
If diagonals of a quadrilateral are equal, it must be a rectangle.
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
