Advertisements
Advertisements
Question
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD
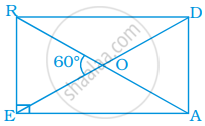
Solution
Given, ∠ROE = 60°
According to given figure,
∠AOE = 120°, ∠AOD = 60° and ∠ROD = 120°.
⇒ In triangle AOE, consider ∠EAR = ∠DEA = x
∠AOE + ∠EAR + ∠DEA = 180°
x + x + 120 = 180°
2x + 120° = 180°
2x = 60°
x = 30°, i.e. ∠EAR = 30°
⇒ In triangle AOD, consider ∠RAD, = ∠EDA = y
∠RAD + ∠EAR + ∠AOD = 180°
y + y + 60° = 180°
2y = 120°
y = 60°, i.e. ∠RAD = 60°.
APPEARS IN
RELATED QUESTIONS
Explain why a rectangle is a convex quadrilateral.
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
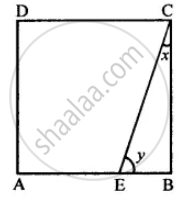
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
Show that the bisectors of angles of a parallelogram form a rectangle
All squares are rectangles.
Every trapezium is a rectangle.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
