Advertisements
Advertisements
प्रश्न
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
पर्याय
100°
150°
105°
120°
उत्तर
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is 150°.
Explanation:
Let EC and FC be altitudes and ∠ECF = 30°.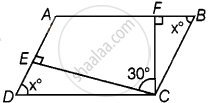
Let ∠EDC = x = ∠FBC
So, ∠ECD = 90° – x and ∠BCF = 90° – x
So, by property of the parallelogram,
∠ADC + ∠DCB = 180°
∠ADC + (∠ECD + ∠ECF + ∠BCF) = 180°
⇒ x + 90° – x + 30° + 90° – x = 180°
⇒ – x = 180° – 210° = – 30°
⇒ x = 30°
Hence, ∠DCB = 30° + 60° + 60° = 150°
APPEARS IN
संबंधित प्रश्न
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
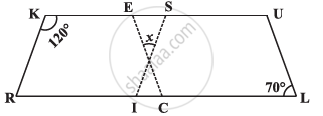
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
All rectangles are parallelograms.
