Advertisements
Advertisements
Question
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
Options
100°
150°
105°
120°
Solution
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is 150°.
Explanation:
Let EC and FC be altitudes and ∠ECF = 30°.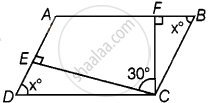
Let ∠EDC = x = ∠FBC
So, ∠ECD = 90° – x and ∠BCF = 90° – x
So, by property of the parallelogram,
∠ADC + ∠DCB = 180°
∠ADC + (∠ECD + ∠ECF + ∠BCF) = 180°
⇒ x + 90° – x + 30° + 90° – x = 180°
⇒ – x = 180° – 210° = – 30°
⇒ x = 30°
Hence, ∠DCB = 30° + 60° + 60° = 150°
APPEARS IN
RELATED QUESTIONS
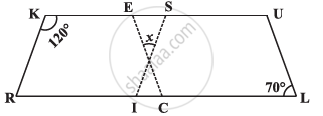
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
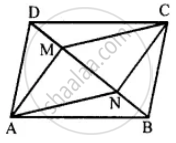
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
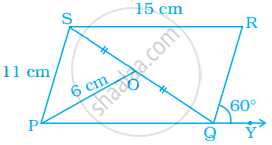
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
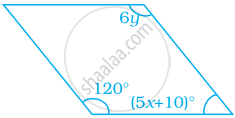
Find the values of x and y in the following parallelogram.
ABCD is a parallelogram. Find the value of x, y and z.

ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
