Advertisements
Advertisements
Question
Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
Solution
Let `square`ABCD be a parallelogram.
AB : BC = 3 : 4
If AB = 3x cm
So, BC = 4x cm ...(x is the common multiple.)
∴ CD = AB = 3x cm and AD = BC = 4x cm ...(opposite sides of parallelogram)
Perimeter of `square`ABCD = 112 cm
∴ AB + BC + CD + AD = 112
∴ 3x + 4x + 3x + 4x = 112
∴ 14x = 112
∴ x = `112/14`
∴ x = 8
∴ CD = AB = 3x = 3 × 8 = 24 cm
∴ AD = BC = 4x = 4 × 8 = 32 cm
APPEARS IN
RELATED QUESTIONS
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
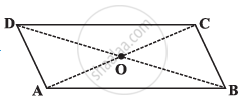
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
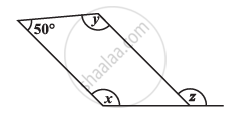
Consider the given parallelogram. Find the values of the unknowns x, y, z.
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
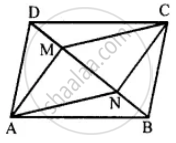
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e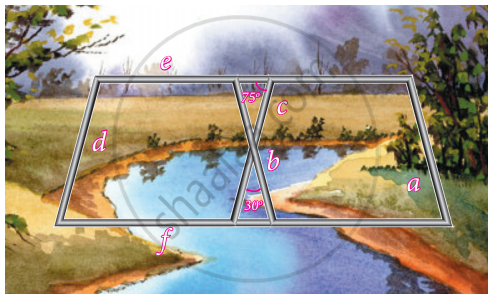
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
