Advertisements
Advertisements
Question
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
Options
1 : 3
2 : 3
1 : 4
1 : 2
Solution
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is 1 : 3.
Explanation:
We know that, adjacent angles of a parallelogram are supplementary, i.e. their sum equals 180°.
∴ (5x – 5) + (10x + 35) = 180°
⇒ 15x + 30° = 180°
⇒ 15x = 150°
⇒ x = 10°
Thus, the angles are (5 × 10 – 5) and (10 × 10 + 35), i.e. 45° and 135°.
Hence, the required ratio is 45° : 135°, i.e. 1 : 3.
APPEARS IN
RELATED QUESTIONS
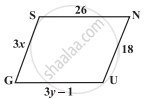
The following figure GUNS is a parallelogram. Find x and y. (Lengths are in cm)
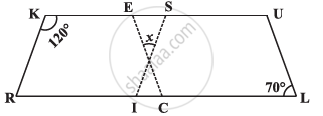
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
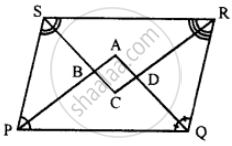
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
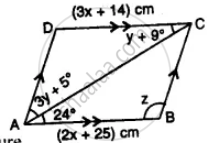
Use the information given in the alongside diagram to find the value of x, y, and z.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

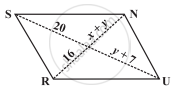
The following figure RUNS is parallelogram. Find x and y. (Lengths are in cm)