Advertisements
Advertisements
Question
A regular pentagon ABCDE and a square ABFG are formed on opposite sides of AB. Find ∠BCF.
Advertisements
Solution
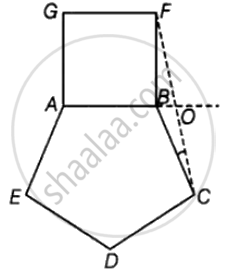
Given, ABCDE is a regular pentagon.
Then, measure of each interior angle of the regular pentagon
= `"Sum of interior angles"/"Number of sides"`
= `((x - 2) xx 180^circ)/5`
= `((5 - 2) xx 180^circ)/5`
= `540^circ/5`
= 108°
∴ ∠CBA = 108°
Join CF,
Now, ∠FBC = 360° – (90° + 108°)
= 360° – 198°
= 162°
In ΔFBC, by the angle sum property, we have
∠FBC + ∠BCF + ∠BFC = 180°
⇒ ∠BCF + ∠BFC = 180° – 162°
⇒ ∠BCF + ∠BFC = 18°
Since, ΔFBC is an isosceles triangle and BF = BC.
∴ ∠BCF = ∠BFC = 9°
APPEARS IN
RELATED QUESTIONS
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
| Figure |  |
 |
 |
 |
| Side | 3 | 4 | 5 | 6 |
| Angle sum | 180° |
2 × 180° = (4 − 2) × 180° |
3 × 180° = (5 − 2) × 180° |
4 × 180° = (6 − 2) × 180° |
What can you say about the angle sum of a convex polygon with number of sides?
a) 7
b) 8
c) 10
d) n
Is it possible to have a regular polygon with measure of each exterior angle as 22°?
Classify the following curve as open or closed:
Find the number of side of a regular polygon, when of its angle has a measure of 160° .
Find the number of side of a regular polygon, when of its angle has a measure of 150° .
Which of the following can never be the measure of exterior angle of a regular polygon?
The measure of each angle of a regular pentagon is ______.
is a polygon.
A polygon is regular if all of its sides are equal.
Find the measure of an are exterior angle of a regular pentagon and an exterior angle of a regular decagon. What is the ratio between these two angles?
