Advertisements
Advertisements
प्रश्न
Find maximum number of acute angles which a convex, a quadrilateral, a pentagon and a hexagon can have. Observe the pattern and generalise the result for any polygon.
उत्तर
If an angle is acute, then the corresponding exterior angle is greater than 90°. Now, suppose a convex polygon has four or more acute angles. Since, the polygon is convex, all the exterior angles are positive, so the sum of the exterior angle is at least the sum of the interior angles. Now, supplementary of the four acute angles, which is greater than 4 × 90° = 360°
However, this is impossible. Since, the sum of exterior angle of a polygon must equal to 360° and cannot be greater than it. It follows that the maximum number of acute angle in convex polygon is 3.
APPEARS IN
संबंधित प्रश्न

The sum of all exterior angles of a triangle is ______.
The number of sides of a regular polygon where each exterior angle has a measure of 45° is ______.
The measure of each exterior angle of a regular polygon of 18 sides is ______.
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is ______.
The number of sides in a regular polygon having measure of an exterior angle as 72° is ______.
The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
The interior angles of a triangle are in the ratio 1:2:3, then the ratio of its exterior angles is 3:2:1.
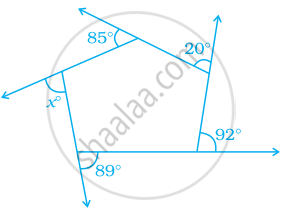
In the figure, find the value of x.