Advertisements
Advertisements
प्रश्न
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is ______.
उत्तर
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is 10.
Explanation:
Given: Exterior angle = 36°
As we know that, the sum of exterior angles of a regular polygon is 360°.
Now, the number of sides is calculated as follows:
Number of sides = `360^circ/"Exterior angle"`
= `360^circ/36^circ`
= 10
APPEARS IN
संबंधित प्रश्न
The sum of all exterior angles of a triangle is ______.
The number of sides of a regular polygon where each exterior angle has a measure of 45° is ______.
Which of the following is not true for an exterior angle of a regular polygon with n sides?
The sum of all exterior angles of a polygon is ______.
The number of sides in a regular polygon having measure of an exterior angle as 72° is ______.
Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
The ratio between exterior angle and interior angle of a regular polygon is 1:5. Find the number of sides of the polygon.
In the figure, find the value of x.
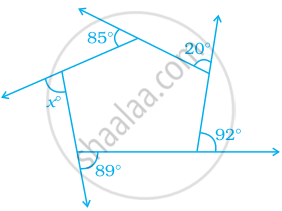
Find maximum number of acute angles which a convex, a quadrilateral, a pentagon and a hexagon can have. Observe the pattern and generalise the result for any polygon.
