Advertisements
Advertisements
प्रश्न
Which of the following can never be the measure of exterior angle of a regular polygon?
विकल्प
22°
36°
45°
30°
उत्तर
22°
Explanation:
Since, we know that, the sum of measures of exterior angles of a polygon is 360°, i.e. measure of each exterior angle = 360°/n, where n is the number of sides/angles.
Thus, measure of each exterior angle will always divide 360° completely.
Hence, 22° can never be the measure of exterior angle of a regular polygon.
APPEARS IN
संबंधित प्रश्न
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
| Figure | 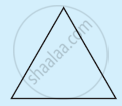 |
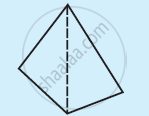 |
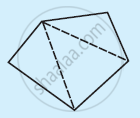 |
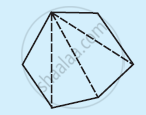 |
| Side | 3 | 4 | 5 | 6 |
| Angle sum | 180° |
2 × 180° = (4 − 2) × 180° |
3 × 180° = (5 − 2) × 180° |
4 × 180° = (6 − 2) × 180° |
What can you say about the angle sum of a convex polygon with number of sides?
a) 7
b) 8
c) 10
d) n
Find the measure of each exterior angle of a regular polygon of 15 sides
Draw rough diagram to illustrate the following Closed curve .
Illustrate, if posible, one of the following with a rough diagram:
A colsed curve that is not a polygon.
Find the number of side of a regular polygon, when of its angle has a measure of 160° .
How many diagonals does a hexagon have?
The name of three-sided regular polygon is ______.
A polygon is regular if all of its sides are equal.
ABCDE is a regular pentagon. The bisector of angle A meets the side CD at M. Find ∠AMC.
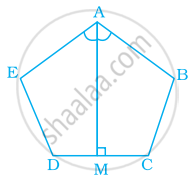
Find the measure of an are exterior angle of a regular pentagon and an exterior angle of a regular decagon. What is the ratio between these two angles?
