Advertisements
Chapters
2: Data Handling
3: Square-Square Root and Cube-Cube Root
▶ 4: Linear Equation In One Variable
5: Understanding Quadrilaterals and Practical Geometry
6: Visualising Solid Shapes
7: Algebraic Expression, Identities and Factorisation
8: Exponents and Powers
9: Comparing Quantities
10: Direct and Inverse Proportions
11: Mensuration
12: Introduct To Graphs
13: Playing With Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 4 - Linear Equation In One Variable NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 4 - Linear Equation In One Variable - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 4: Linear Equation In One Variable
Below listed, you can find solutions for Chapter 4 of CBSE NCERT Exemplar for Mathematics [English] Class 8.
NCERT Exemplar solutions for Mathematics [English] Class 8 4 Linear Equation In One Variable Exercise [Pages 110 - 121]
Choose the correct alternative:
The solution of which of the following equations is neither a fraction nor an integer.
3x + 2 = 5x + 2
4x – 18 = 2
4x + 7 = x + 2
5x – 8 = x + 4
The solution of the equation ax + b = 0 is ______.
` x = a/b`
`x = -b`
`x = (-b)/a`
`x = b/a`
If 8x – 3 = 25 + 17x, then x is ______.
a fraction
an integer
a rational number
cannot be solved
The shifting of a number from one side of an equation to other is called ______.
Transposition
Distributivity
Commutativity
Associativity
If `(5x)/3 - 4 = (2x)/5`, then the numerical value of 2x – 7 is ______.
`19/13`
`- 13/19`
0
`13/19`
The value of x for which the expressions 3x – 4 and 2x + 1 become equal is ______.
–3
0
5
1
If a and b are positive integers, then the solution of the equation ax = b has to be always ______.
positive
negative
one
zero
Linear equation in one variable has ______
only one variable with any power.
only one term with a variable.
only one variable with power 1.
only constant term.
Which of the following is a linear expression?
x2 + 1
y + y2
4
1 + z
A linear equation in one variable has ______.
Only one solution
Two solutions
More than two solutions
No solution
Value of S in `1/3` + S = `2/5` is ______.
`4/5`
`1/15`
10
0
`(-4)/3 y = - 3/4`, then y = ______.
`-(3/4)^2`
`-(4/3)^2`
`(3/4)^2`
`(4/3)^2`
The digit in the tens place of a two-digit number is 3 more than the digit in the units place. Let the digit at units place be b. Then the number is ______.
11b + 30
10b + 30
11b + 3
10b + 3
Arpita’s present age is thrice of Shilpa. If Shilpa’s age three years ago was x. Then Arpita’s present age is ______.
3(x – 3)
3x + 3
3x – 9
3(x + 3)
The sum of three consecutive multiples of 7 is 357. Find the smallest multiple.
112
126
119
116
Fill in the blanks:
In a linear equation, the ______ power of the variable appearing in the equation is one.
The solution of the equation 3x – 4 = 1 – 2x is ______.
The solution of the equation `2y = 5y - 18/5` is ______.
Any value of the variable which makes both sides of an equation equal is known as a ______ of the equation.
9x – ______ = –21 has the solution (–2)
Three consecutive numbers whose sum is 12 are ______, ______ and ______.
The share of A when Rs 25 are divided between A and B so that A gets Rs. 8 more than B is ______.
A term of an equation can be transposed to the other side by changing its ______.
On subtracting 8 from x, the result is 2. The value of x is ______.
`x/5 + 30 = 18` has the solution as ______.
When a number is divided by 8, the result is –3. The number is ______.
9 is subtracted from the product of p and 4, the result is 11. The value of p is ______.
If `2/5 x - 2 = 5 - 3/5 x`, then x = ______.
After 18 years, Swarnim will be 4 times as old as he is now. His present age is ______.
Convert the statement Adding 15 to 4 times x is 39 into an equation ______.
The denominator of a rational number is greater than the numerator by 10. If the numerator is increased by 1 the and denominator is decreased by 1, then expression for new denominator is ______.
The sum of two consecutive multiples of 10 is 210. The smaller multiple is ______.
State whether the following statement is True or False:
3 years ago, the age of a boy was y years. His age 2 years ago was (y – 2) years.
True
False
Shikha’s present age is p years. Reemu’s present age is 4 times the present age of Shikha. After 5 years Reemu’s age will be 15p years.
True
False
In a 2 digit number, the units place digit is x. If the sum of digits be 9, then the number is (10x – 9).
True
False
Sum of the ages of Anju and her mother is 65 years. If Anju’s present age is y years then her mother’s age before 5 years is (60 – y) years.
True
False
The number of boys and girls in a class are in the ratio 5 : 4. If the number of boys is 9 more than the number of girls, then number of boys is 9.
True
False
A and B are together 90 years old. Five years ago A was thrice as old as B was. Hence, the ages of A and B five years back would be (x – 5) years and (85 – x) years respectively.
True
False
Two different equations can never have the same answer.
True
False
In the equation 3x – 3 = 9, transposing –3 to RHS, we get 3x = 9.
True
False
In the equation 2x = 4 – x, transposing – x to LHS, we get x = 4.
True
False
If `15/8 - 7x = 9`, then `-7x = 9 + 15/8`
True
False
If `x/3 + 1 = 7/15`, then `x/3 = 6/15`
True
False
If 6x = 18, then 18x = 54
True
False
If `x/11 = 15`, then `x = 11/15`
True
False
If x is an even number, then the next even number is 2(x + 1).
True
False
If the sum of two consecutive numbers is 93 and one of them is x, then the other number is 93 – x.
True
False
Two numbers differ by 40, when each number is increased by 8, the bigger becomes thrice the lesser number. If one number is x, then the other number is (40 – x).
True
False
Solve the following:
`(3x - 8)/(2x) = 1`
Solve the following:
`(5x)/(2x - 1) = 2`
Solve the following:
`(2x - 3)/(4x + 5) = 1/3`
Solve the following:
`8/x = 5/(x - 1)`
Solve the following:
`(5(1 - x) + 3(1 + x))/(1 - 2x) = 8`
Solve the following:
`(0.2x + 5)/(3.5x - 3) = 2/5`
Solve the following:
`(y - (4 - 3y))/(2y - (3 + 4y)) = 1/5`
Solve the following:
`x/5 = (x - 1)/6`
Solve the following:
0.4(3x – 1) = 0.5x + 1
Solve the following:
8x – 7 – 3x = 6x – 2x – 3
Solve the following:
10x – 5 – 7x = 5x + 15 – 8
Solve the following:
4t – 3 – (3t + 1) = 5t – 4
Solve the following:
5(x – 1) – 2(x + 8) = 0
Solve the following:
`x/2 - 1/4(x - 1/3) = 1/6(x + 1) + 1/12`
Solve the following:
`1/2(x + 1) + 1/3(x - 1) = 5/12(x - 2)`
Solve the following:
`(x + 1)/4 = (x - 2)/3`
Solve the following:
`(2x - 1)/5 = (3x + 1)/3`
Solve the following:
1 – (x – 2) – [(x – 3) – (x – 1)] = 0
Solve the following:
`3x - (x - 2)/3 = 4 - (x - 1)/4`
Solve the following:
`(3t + 5)/4 - 1 = (4t - 3)/5`
Solve the following:
`(2y - 3)/4 - (3y - 5)/2 = y + 3/4`
Solve the following:
0.25(4x – 5) = 0.75x + 8
Solve the following:
`(9 - 3y)/(1 - 9y) = 8/5`
Solve the following:
`(3x + 2)/(2x - 3) = - 3/4`
Solve the following:
`(5x + 1)/(2x) = - 1/3`
Solve the following:
`(3t - 2)/3 + (2t + 3)/2 = t + 7/6`
Solve the following:
`m - (m - 1)/2 = 1 - (m - 2)/3`
Solve the following:
4(3p + 2) – 5(6p – 1) = 2(p – 8) – 6(7p – 4)
Solve the following:
3(5x – 7) + 2(9x – 11) = 4(8x – 7) – 111
Solve the following:
0.16(5x – 2) = 0.4x + 7
Radha takes some flowers in a basket and visits three temples one by one. At each temple, she offers one-half of the flowers from the basket. If she is left with 3 flowers at the end, find the number of flowers she had in the beginning.
Rs. 13500 are to be distributed among Salma, Kiran and Jenifer in such a way that Salma gets Rs. 1000 more than Kiran and Jenifer gets Rs. 500 more than Kiran. Find the money received by Jenifer.
The volume of water in a tank is twice of that in the other. If we draw out 25 litres from the first and add it to the other, the volumes of the water in each tank will be the same. Find the volume of water in each tank.
Anushka and Aarushi are friends. They have equal amount of money in their pockets. Anushka gave `1/3` of her money to Aarushi as her birthday gift. Then Aarushi gave a party at a restaurant and cleared the bill by paying half of the total money with her. If the remaining money in Aarushi’s pocket is Rs.1600, find the sum gifted by Anushka.
Kaustubh had 60 flowers. He offered some flowers in a temple and found that the ratio of the number of remaining flowers to that of flowers in the beginning is 3:5. Find the number of flowers offered by him in the temple.
The sum of three consecutive even natural numbers is 48. Find the greatest of these numbers.
The sum of three consecutive odd natural numbers is 69. Find the prime number out of these numbers.
The sum of three consecutive numbers is 156. Find the number which is a multiple of 13 out of these numbers.
Find a number whose fifth part increased by 30 is equal to its fourth part decreased by 30.
Divide 54 into two parts such that one part is `2/7` of the other.
Sum of the digits of a two-digit number is 11. The given number is less than the number obtained by interchanging the digits by 9. Find the number.
Two equal sides of a triangle are each 4 m less than three times the third side. Find the dimensions of the triangle, if its perimeter is 55 m.
After 12 years, Kanwar shall be 3 times as old as he was 4 years ago. Find his present age.
Anima left one-half of her property to her daughter, one-third to her son and donated the rest to an educational institute. If the donation was worth Rs. 1,00,000, how much money did Anima have?
If `1/2` is subtracted from a number and the difference is multiplied by 4, the result is 5. What is the number?
The sum of four consecutive integers is 266. What are the integers?
Hamid has three boxes of different fruits. Box A weighs `2 1/2` kg more than Box B and Box C weighs `10 1/4` kg more than Box B. The total weight of the three boxes is `48 3/4` kg. How many kilograms (kg) does Box A weigh?
The perimeter of a rectangle is 240 cm. If its length is increased by 10% and its breadth is decreased by 20%, we get the same perimeter. Find the length and breadth of the rectangle.
The age of A is five years more than that of B. 5 years ago, the ratio of their ages was 3 : 2. Find their present ages.
If numerator is 2 less than denominator of a rational number and when 1 is subtracted from numerator and denominator both, the rational number in its simplest form is `1/2`. What is the rational number?
In a two-digit number, digit in units place is twice the digit in tens place. If 27 is added to it, digits are reversed. Find the number.
A man was engaged as typist for the month of February in 2009. He was paid Rs. 500 per day but Rs. 100 per day were deducted for the days he remained absent. He received Rs. 9,100 as salary for the month. For how many days did he work?
A steamer goes downstream and covers the distance between two ports in 3 hours. It covers the same distance in 5 hours when it goes upstream. If the stream flows at 3 km/hr, then find what is the speed of the steamer upstream?
A lady went to a bank with Rs. 1,00,000. She asked the cashier to give her Rs. 500 and Rs. 1,000 currency notes in return. She got 175 currency notes in all. Find the number of each kind of currency notes.
There are 40 passengers in a bus, some with Rs. 3 tickets and remaining with Rs. 10 tickets. The total collection from these passengers is Rs. 295. Find how many passengers have tickets worth Rs. 3?
Denominator of a number is 4 less than its numerator. If 6 is added to the numerator it becomes thrice the denominator. Find the fraction.
An employee works in a company on a contract of 30 days on the condition that he will receive Rs. 120 for each day he works and he will be fined Rs. 10 for each day he is absent. If he receives Rs. 2300 in all, for how many days did he remain absent?
Kusum buys some chocolates at the rate of Rs. 10 per chocolate. She also buys an equal number of candies at the rate of Rs. 5 per candy. She makes a 20% profit on chocolates and 8% profit on candies. At the end of the day, all chocolates and candies are sold out and her profit is Rs. 240. Find the number of chocolates purchased.
A steamer goes downstream and covers the distance between two ports in 5 hours while it covers the same distance upstream in 6 hours. If the speed of the stream is 1 km/hr, find the speed of the steamer in still water.
Distance between two places A and B is 210 km. Two cars start simultaneously from A and B in opposite direction and distance between them after 3 hours is 54 km. If speed of one car is less than that of other by 8 km/hr, find the speed of each.
A carpenter charged Rs. 2500 for making a bed. The cost of materials used is Rs. 1100 and the labour charges are Rs. 200/hr. For how many hours did the carpenter work?
For what value of x is the perimeter of shape 77 cm?
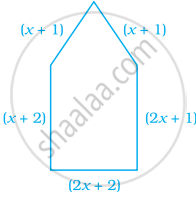
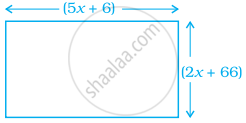
For what value of x is the perimeter of shape 186 cm?
On dividing Rs. 200 between A and B such that twice of A’s share is less than 3 times B’s share by 200, B’s share is?
Madhulika thought of a number, doubled it and added 20 to it. On dividing the resulting number by 25, she gets 4. What is the number?
Solutions for 4: Linear Equation In One Variable
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 4 - Linear Equation In One Variable NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 4 - Linear Equation In One Variable - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 4 - Linear Equation In One Variable
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 8 CBSE 4 (Linear Equation In One Variable) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 4 Linear Equation In One Variable are Reducing Equations to Simpler Form, Linear Equation in One Variable, Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side, Some Applications Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side, Solving Equations Having the Variable on Both Sides, Some More Applications on the Basis of Solving Equations Having the Variable on Both Sides, The Solution of an Equation, Variable of Equation, Concept of Equation, Expressions with Variables, Balancing an Equation, Equations Reducible to the Linear Form.
Using NCERT Exemplar Mathematics [English] Class 8 solutions Linear Equation In One Variable exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 4, Linear Equation In One Variable Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
