Advertisements
Advertisements
प्रश्न
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is ______.
विकल्प
25 cm
20 cm
26 cm
3.5 cm
उत्तर
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is 26 cm.
Explanation:
In ΔBCD,
∠BDC = 90°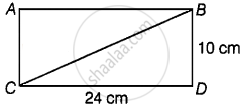
∴ Using Pythagoras theorem,
We have, BC2 = BD2 + CD2
⇒ BC2 = 102 + 242
⇒ BC2 = 100 + 576
⇒ BC2 = 676
⇒ BC = `sqrt(676)`
⇒ BC = 26 cm
APPEARS IN
संबंधित प्रश्न
The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
Prove that the bisectors of interior angles of a parallelogram form a rectangle.
The diagonals PR and QS of a quadrilateral PQRS are perpendicular to each other. A, B, C and D are mid-point of PQ, QR, RS and SP respectively. Prove that ABCD is a rectangle.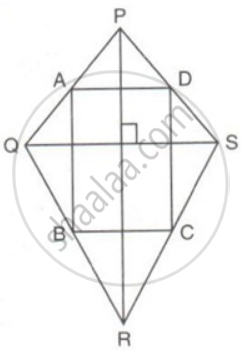
PQRS is a parallelogram. M and N are the mid-points of the adjacent sides QR and RS. O is the mid-point of the diagonal PR. Prove that MONR is a rectangle and MN is half of PR.
ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: areaΔAOD + areaΔBOC + areaΔABO + areaΔCDO.
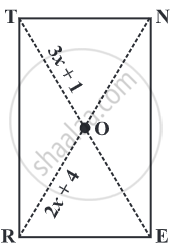
Diagonals of a rectangle are ______.
If one diagonal of a rectangle is 6 cm long, length of the other diagonal is ______.
Diagonals of a rectangle are equal.
Diagonals of rectangle bisect each other at right angles.
