Advertisements
Advertisements
प्रश्न
The diagonals PR and QS of a quadrilateral PQRS are perpendicular to each other. A, B, C and D are mid-point of PQ, QR, RS and SP respectively. Prove that ABCD is a rectangle.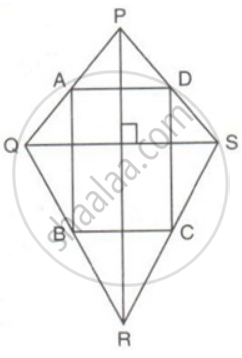
उत्तर
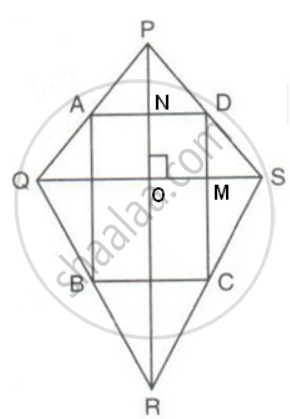
In ΔPQS, A and D are mid-points of sides QP and PS respectively.
Therefore, AD || QS and AD = `(1)/(2)"QS"` ..........(i)
In ΔQRS
B and C are the mid-points of QR and RS respectively
Therefore, BC || QS and BC = `(1)/(2)"QS"` ..........(ii)
From equations (i) and (ii),
AD || BC and AD = BC
As in quadrilateral ABCD one pair of opposite sides are equal and parallel to each other, so it is parallelogram.
The diagonals of quadrilateral PQRS intersect each other at point O.
Now in quadrilateral OMDN
ND || OM ...( AD || QS)
DM || ON ...(DC || PR)
So, OMDN is parallelogram
∠MDN = ∠NOM
∠ADC =∠NOM
But, ∠NOM = 90° ...(doagonals are perpendicular to each other)
⇒ ∠ADC = 90°
Clearly ABCD is a parallelogram having one of its interior angle as 90°.
Hence, ABCD is rectangle.
APPEARS IN
संबंधित प्रश्न
The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
Prove that the bisectors of interior angles of a parallelogram form a rectangle.
PQRS is a parallelogram. M and N are the mid-points of the adjacent sides QR and RS. O is the mid-point of the diagonal PR. Prove that MONR is a rectangle and MN is half of PR.
ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: areaΔAOD + areaΔBOC + areaΔABO + areaΔCDO.
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is ______.
Diagonals of a rectangle are ______.
If one diagonal of a rectangle is 6 cm long, length of the other diagonal is ______.
Diagonals of rectangle bisect each other at right angles.
A photo frame is in the shape of a quadrilateral. With one diagonal longer than the other. Is it a rectangle? Why or why not?
