Advertisements
Advertisements
प्रश्न
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
उत्तर
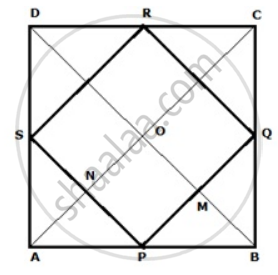
Join AC and BD
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
Therefore, PQ || AC and PQ = `(1)/(2)"AC"`.......(i)
In ΔADC, R and S are the mid-points of sides CD and AD respectively.
Therefore, RS || AC and RS = `(1)/(2)"AC"`.......(ii)
From (i) and (ii)
PQ || RS and PQ = RS ............(iii)
Thus, in a quadrilateral PQRS one pair of opposite sides are equal and parallel.
Hence, PQRS is a parallelogram.
Since ABCD is a square
AB = BC = CD = DA
= `(1)/(2)"AB" = (1)/(2)"CD";(1)/(2)"AB" = (1)/(2)`
⇒ PB = RC;BQ = CQ
Thus in ΔPBQ and ΔRCQ,
PB = RC
BQ = CQ
∠PBQ = ∠RCQ = 90°
Therefore, ΔPBQ ≅ ΔRCQ
Hence, PQ = QR ........(iv)
From (iii) and (iv)
PQ = QR = RS
But PQRS is a parallelogram
⇒ QR = PS
⇒ PQ = QR = RS = PS .......(v)
Now, PQ || AC
⇒ PM || NO ........(vi)|
Since P and S are the mid-points of AB and AD respectively
PS || BD
⇒ PN || MO .........(vii)
Thus in quadrilateral PMON,
PM || NO ...(from (vi))
PN || MO ...)from (vii))
So, PMON is a parallelogram
⇒ ∠MPN = ∠MON
⇒ ∠MPN = ∠BOA
⇒ ∠MPN = 90° ...(⊥∵ diagonals)
⇒ ∠QPS = 90°
Thus, PQRS is a quadrilateral such that PQ = QR = RS = PS and ∠QPS = 90°
Hence, PQRS is a square.
APPEARS IN
संबंधित प्रश्न
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.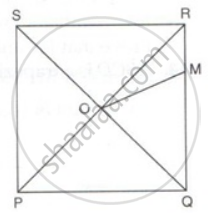
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.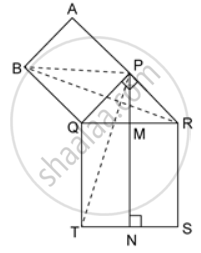
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.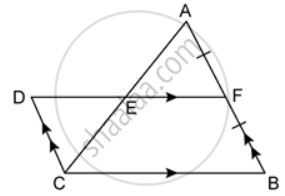
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
