Advertisements
Advertisements
प्रश्न
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
उत्तर
Given, EFGH is a rectangle in which diagonals are intersecting at the point J.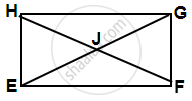
We know that, the diagonals of a rectangle bisect each other and are equal.
Then, EG = 2 × JF
⇒ 24x – 8 = 2(8x + 4)
⇒ 24x – 8 = 16x + 8
⇒ 24x – 16x = 8 + 8
⇒ 8x = 16
⇒ x = 2
APPEARS IN
संबंधित प्रश्न
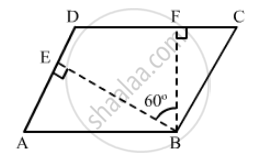
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
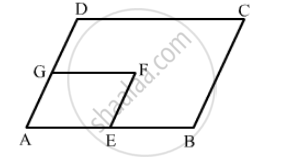
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rectangle.
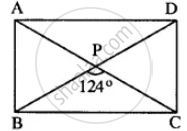
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
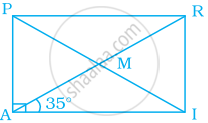
In rectangle PAIR, find ∠ARI, ∠RMI and ∠PMA.
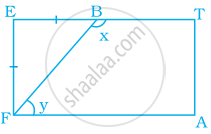
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.