Advertisements
Advertisements
Question
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
Solution
\[\text{ Opposite angles of a parallelogram are equal } . \]
\[ \therefore \angle C = 70° = \angle A . \]
\[ \angle B = \angle D\]
\[\text{ Also, the sum of the adjacent angles of a parallelogram is } 180°. \]
\[ \therefore \angle A + \angle B = 180°\]
\[70° + \angle B = 180°\]
\[\angle B = 110°\]
\[ \therefore \angle B = 110°, \angle C = 70°\text{ and } \angle D = 110°\]
APPEARS IN
RELATED QUESTIONS
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
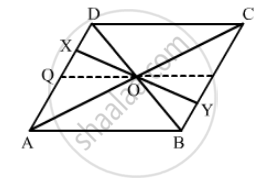
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
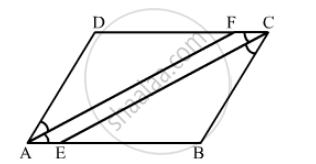
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
Its diagonals are equal and perpendicular.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.
