Advertisements
Advertisements
प्रश्न
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
उत्तर
\[\text{ Let the angles be A, B, C and D }. \]
\[\text{ It is given that the sum of two opposite angles is } 130°. \]
\[ \therefore \angle A + \angle C = 130°\]
\[\angle A + \angle A = 130° \left( \text{ opposite angles of a parallelogram are same } \right)\]
\[\angle A = 65°\]
\[\text{ and } \angle C = 65°\]
\[\text{ The sum of adjacent angles of a paralle\logram is } 180° . \]
\[\angle A + \angle B = 180°\]
\[65°+ \angle B = 180°\]
\[\angle B = 180°- 65°\]
\[\angle B = 115°\]
\[ \angle D = 115°\]
\[ \therefore \angle A = 65°, v\angle B = 115°, \angle C = 65° \text{ and } \angle D = 115° .\]
APPEARS IN
संबंधित प्रश्न
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
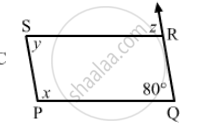
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
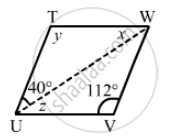
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
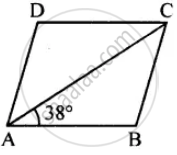
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
