Advertisements
Advertisements
Question
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
Solution
Given, AB = 25 cm and BC = 15 cm
Now, In rectangle ABCD,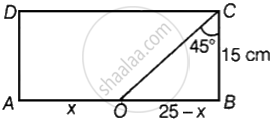
CO is the bisector of ∠C and it divides AB.
∴ ∠OCB = ∠OCD = 45°
∴ ∠OCB = ∠OCD = 45°
In ΔOCB, we have
∠CBO + ∠OCB + ∠COB = 180° ...[Angle sum property of triangle]
90° + 45° + ∠COB = 180°
∠COB = 180° – 90° + 45°
∠COB = 180° – 135° = 45°
Now, In ΔOCB,
∠OCB = ∠COB
Then, OB = OC
⇒ OB = 15 cm
CO divides AB in the ratio AO : OB
Let AO be x, then OB = AB – x = 25 – x
Hence, AO : OB = x : 25 – x
⇒ 10 : 15
⇒ 2 : 3
APPEARS IN
RELATED QUESTIONS
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement is true for a rectangle?
Its diagonals are equal.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
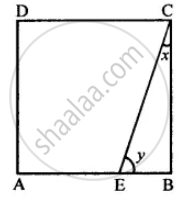
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
For which of the following figures, all angles are equal?
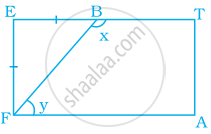
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
