Advertisements
Advertisements
प्रश्न
Prove that the bisectors of the interior angles of a rectangle form a square.
उत्तर
Given: A parallelogram ABCD in which AR, BR, CP, DP are the bisects of ∠A, ∠B, ∠C, ∠D, respectively forming quadrilaterals PQRS.
To prove: PQRS is a square.
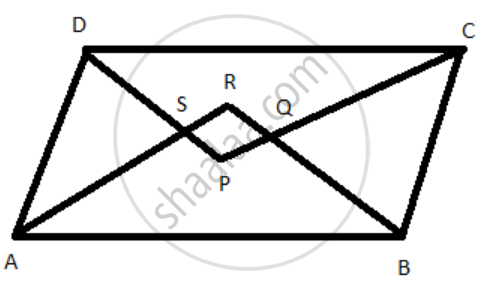
Proof:
In Δ ARB,
∠RAB + ∠RBA + ∠ARB = 180°
45° + 45° + ∠ARB = 180°
90° + ∠ARB = 180°
∠ARB = 180° - 90°
∴ ∠ARB = 90°
Similarly, ∠SRQ = 90°
In Δ ARB,
AR = BR ...(i)
ΔASD ≅ Δ BQC ...[By ASA rule]
AS = BQ ...(ii) [by CPCTC]
(i) - (ii)
AR - AS = BR - BQ
SR = RQ ...(iii)
Also, SP = PQ ...(iv)
PQ = RS ...(v)
Hence, PQRS is a square.
APPEARS IN
संबंधित प्रश्न
All squares are not parallelograms.
Identify all the quadrilaterals that have four right angles
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
Explain how a square is a rectangle
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.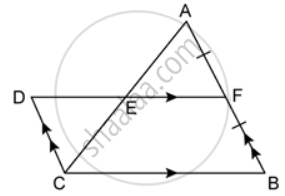
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
