Advertisements
Advertisements
प्रश्न
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
उत्तर
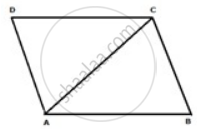
ABCD is a parallelogram.
Let ∠CAB = x°
Then, ∠ABC = 5x° and ∠BCA = 3x°
In ΔABC,
∠CAB + ∠ABC + ∠BCA = 180° ...(sum of angles of triangle = 180°)
x° + 5x° + 3x° = 180°
9x° = 180°
x° = 20°
⇒ ∠CAB = x° = 20°
⇒ ∠ABC = 5x° = 5 x 20° = 100°
⇒ ∠ BCA = 3x° = 3 x 20° = 60°
Now,
∠ADC = ∠ABC = 100° ...(opposite angles of a parallelogram are equal)
∠ACD =∠CAB = 20° ...(Alternate angles since BC || AD)
∠ CAD = ∠BCA = 60° ...(Alternate angles since BC || AD)
Therefore,
∠ADC= ∠ABC = 100°, ∠ACD + ∠BCA = 80°, ∠CAD + ∠CAB = 80°.
APPEARS IN
संबंधित प्रश्न
In the following figure, ABCD and PQRS are two parallelograms such that ∠D = 120° and ∠Q = 70°.
Find the value of x.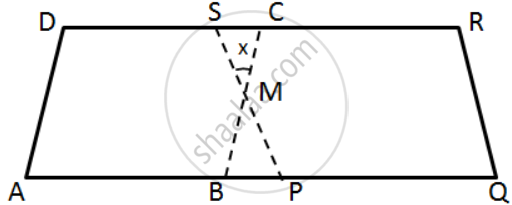
In case of a parallelogram
prove that:
(i) The bisectors of any two adjacent angles intersect at 90o.
(ii) The bisectors of the opposite angles are parallel to each other.
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
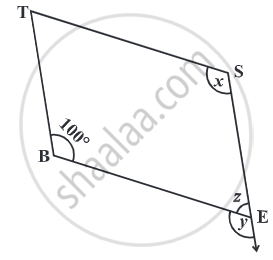
In the following figures, find the remaining angles of the parallelogram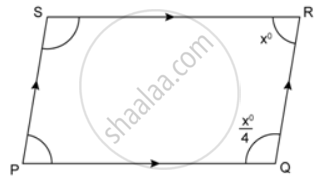
In the following figures, find the remaining angles of the parallelogram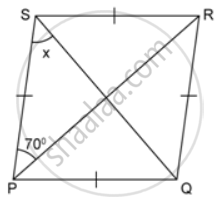
In the given figure, ABCD is a parallelogram, find the values of x and y.
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
The sum of adjacent angles of a parallelogram is ______.
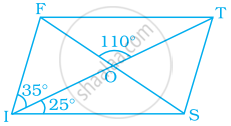
In parallelogram FIST, find ∠SFT, ∠OST and ∠STO.