Advertisements
Advertisements
प्रश्न
In case of a parallelogram
prove that:
(i) The bisectors of any two adjacent angles intersect at 90o.
(ii) The bisectors of the opposite angles are parallel to each other.
उत्तर

ABCD is a parallelogram, the bisectors of ∠ADC and ∠BCD meet at a point E and the bisectors of ∠BCD and ∠ABC meet at F.
We have to prove that the ∠CED = 90° and ∠CFG = 90°
Proof: In the parallelogram ABCD
∠ADC + ∠BCD = 180° ....[ sum of adjacent angles of a parallelogram ]
⇒ `"∠ADC"/2 + "∠BCD"/2` = 90°
⇒ ∠EDC + ∠ECD + ∠CED = 180°
⇒ ∠CED = 90°
Similarly taking triangle BCF it can be proved that ∠BFC = 90°
∠BFC + ∠CFG = 180° ....[ adjacent angles on a line ]
Also ⇒ ∠CFG = 90°
Now since ∠CFG = ∠CED = 90° ....[ It means that the lines DE and BG are parallel ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D.
In the given figure, AP is the bisector of ∠A and CQ is the bisector of ∠C of parallelogram ABCD. 
Prove that APCQ is a parallelogram.
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
In the following figures, find the remaining angles of the parallelogram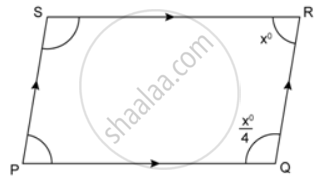
In the following figures, find the remaining angles of the parallelogram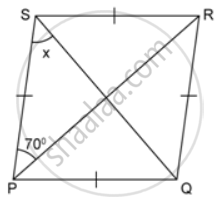
In a parallelogram ABCD ∠C = 98°. Find ∠A and ∠B.
The consecutive angles of a parallelogram are in the ratio 3:6. Calculate the measures of all the angles of the parallelogram.
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
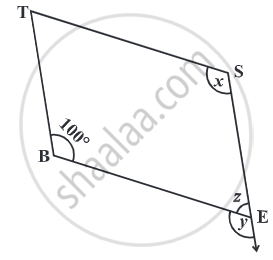
The sum of adjacent angles of a parallelogram is ______.
