Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD ∠C = 98°. Find ∠A and ∠B.
उत्तर
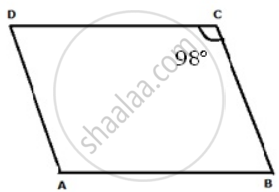
ABCD is a parallelogram
∠C = 98°
∴ ∠A = ∠C = 98° ....(opposite angles of a parallelogram are equal)
∠A + ∠B +∠C + ∠D = 360° ....(Sum of all angles of a quadrilateral = 360°)
98° + ∠B + 98° + ∠D = 360°
∠B + 196 + ∠D = 360°
∠B + ∠D = 360° - 196°
∠B +∠D = 164°
But ∠B = ∠D ....(opposite angles of a parallelogram are equal)
⇒ 2∠B = 164°
⇒ ∠B = 82° = ∠D
Therefore,
∠B = 82°, ∠A = 98°.
APPEARS IN
संबंधित प्रश्न
In case of a parallelogram
prove that:
(i) The bisectors of any two adjacent angles intersect at 90o.
(ii) The bisectors of the opposite angles are parallel to each other.
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
In the following figures, find the remaining angles of the parallelogram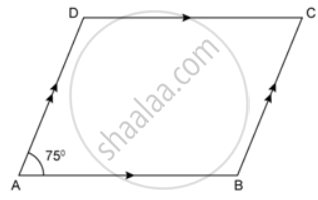
In the following figures, find the remaining angles of the parallelogram
In the following figures, find the remaining angles of the parallelogram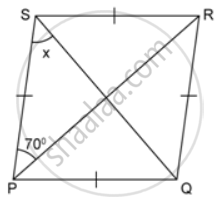
Find the measures of all the angles of the parallelogram shown in the figure: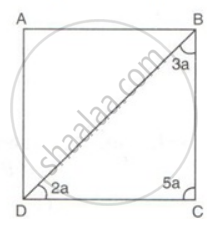
In the given figure, ABCD is a parallelogram, find the values of x and y.
PQR is a triangle formed by the adjacent sides PQ and QR and diagonal PR of a parallelogram PQRS. If in ΔPQR, ∠P : ∠Q : ∠R = 3 : 8 : 4, Calculate the measures of all the angles of parallelogram PQRS.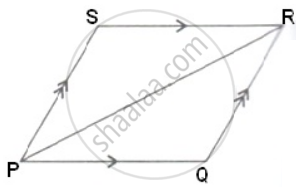
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
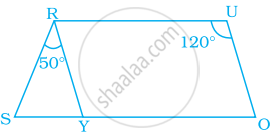
In the given parallelogram YOUR, ∠RUO = 120° and OY is extended to point S such that ∠SRY = 50°. Find ∠YSR.