Advertisements
Advertisements
प्रश्न
Find the measures of all the angles of the parallelogram shown in the figure: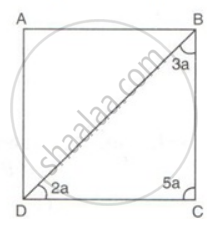
उत्तर
In ΔBDC,
∠BDC + ∠DCB + ∠CBD = 180°
2a + 5a + 3a = 180°
10a = 180°
⇒ a = 18°
∠BDC = 2a = 2x 18° = 36°
∠DCB = 5a = 5 x 18° = 90°
∠CBD = 3a = 3 x 18° = 54°
∠DAB =∠DCB = 90° ...(opposite angles of parallelogram are equal)
∠DBA = ∠BDC = 36° ...(alternate angles since AB || CD)
∠BDA = ∠CBD = 54° ...(alternate angles since AB || CD)
Therefore, ∠DAB =∠DCB = 90°, ∠DBA + ∠CBD = 90°, ∠BDA + ∠BDC = 90°.
APPEARS IN
संबंधित प्रश्न
In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D.
In the following figure, ABCD and PQRS are two parallelograms such that ∠D = 120° and ∠Q = 70°.
Find the value of x.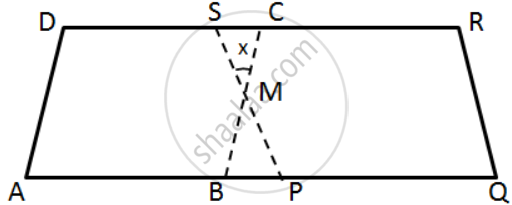
In case of a parallelogram
prove that:
(i) The bisectors of any two adjacent angles intersect at 90o.
(ii) The bisectors of the opposite angles are parallel to each other.
In the following figures, find the remaining angles of the parallelogram
In the following figures, find the remaining angles of the parallelogram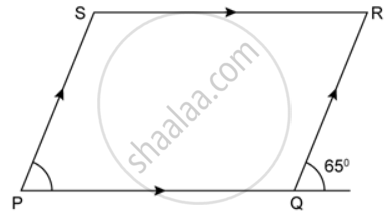
In the following figures, find the remaining angles of the parallelogram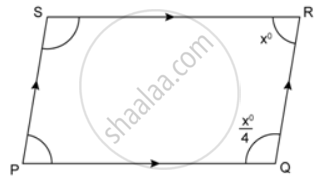
In the given figure, ABCD is a parallelogram, find the values of x and y.
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
The sum of adjacent angles of a parallelogram is ______.
