Advertisements
Advertisements
प्रश्न
The consecutive angles of a parallelogram are in the ratio 3:6. Calculate the measures of all the angles of the parallelogram.
उत्तर
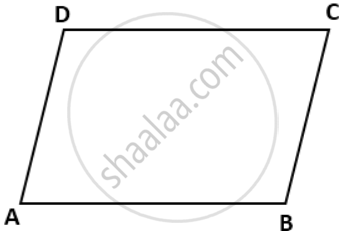
Let ABCD is a parallelogram in which AD || BC.
∠A and ∠B are consecutive angles:
∠A : ∠B = 3 : 6
∴ ∠A = 3x and ∠B = 6x
AD || BC and AB is the transversal.
⇒ ∠A + ∠B = 180° ....(Co-interior angles are supplementary)
⇒ 3x + 6x = 180°
⇒ 9x = 180°
⇒ x = 20
∴ ∠A = 3 x 20° = 60° and ∠B = 6 x 20° = 120°
Since opposite angles of a parallelogram are equal.
∴ ∠C =∠A = 60° and ∠D = ∠B = 120°.
APPEARS IN
संबंधित प्रश्न
In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D.
In the following figure, ABCD and PQRS are two parallelograms such that ∠D = 120° and ∠Q = 70°.
Find the value of x.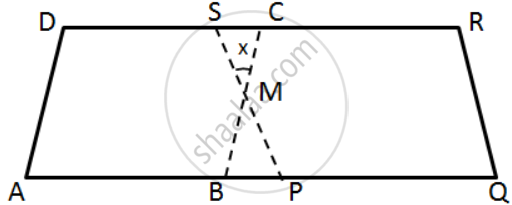
In case of a parallelogram
prove that:
(i) The bisectors of any two adjacent angles intersect at 90o.
(ii) The bisectors of the opposite angles are parallel to each other.
In the given figure, AP is the bisector of ∠A and CQ is the bisector of ∠C of parallelogram ABCD. 
Prove that APCQ is a parallelogram.
In the following figures, find the remaining angles of the parallelogram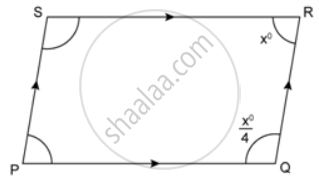
Find the measures of all the angles of the parallelogram shown in the figure: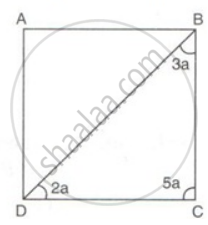
In the given figure, ABCD is a parallelogram, find the values of x and y.
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
