Advertisements
Advertisements
प्रश्न
The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
उत्तर

To prove: ABCD is a square,
that is, to prove that sides of the quadrilateral are equal
and each angle of the quadrilateral is 90°,
ABCD is a rectangle,
⇒ ∠A = ∠B = ∠c = ∠D = 90° and diagonals bisect each other.
that is, MD = BM ....(i)
Consider ΔAMD and ΔAMB,
MD = BM ....( from(i) )
∠AMD = ∠AMB = 90° .....(given)
AM = AM ......( common side )
ΔAMD ≅ ΔAMB ....(SAS ngruence iterion)
⇒ AD = AB ....( c.p.c.t.c. )
Since ABCD is a rectangle, AD = BC and AB = CD
Thus, AB = BC = CD = AD and ∠A = ∠B = ∠C = ∠D = 90°
⇒ ABCD is a square.
APPEARS IN
संबंधित प्रश्न
Prove that the bisectors of interior angles of a parallelogram form a rectangle.
The diagonals PR and QS of a quadrilateral PQRS are perpendicular to each other. A, B, C and D are mid-point of PQ, QR, RS and SP respectively. Prove that ABCD is a rectangle.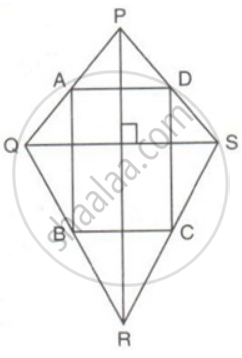
PQRS is a parallelogram. M and N are the mid-points of the adjacent sides QR and RS. O is the mid-point of the diagonal PR. Prove that MONR is a rectangle and MN is half of PR.
ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: areaΔAOD + areaΔBOC + areaΔABO + areaΔCDO.
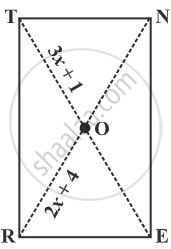
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is ______.
Diagonals of a rectangle are ______.
If one diagonal of a rectangle is 6 cm long, length of the other diagonal is ______.
Diagonals of rectangle bisect each other at right angles.
A photo frame is in the shape of a quadrilateral. With one diagonal longer than the other. Is it a rectangle? Why or why not?
