Advertisements
Advertisements
Question
In the following figures, find the remaining angles of the parallelogram
Solution
PQRS is a parallelogram.
∠Q = 60°
⇒ ∠S = 60° ....(Opposite angles of a parallelogram are equal)
In ΔPQR,
∠RPQ + ∠PQR + ∠PRQ = 180° ....(Angle sum property of a triangle)
⇒ 50° + 60°+ ∠PRQ = 180°
⇒ 110° + ∠PRQ = 180°
⇒ ∠PRQ = 70°
And, ∠SPR = ∠PRQ = 70° ....(Alternate angles)
⇒ ∠SPQ
= ∠SPR + ∠RPQ
= 70° + 50°
= 120°
⇒ ∠SRQ = 120° ....(Opposite angles of a parallelogram are equal)
Thus, we have
∠P = 120°, ∠S = 60° and ∠R =120°.
APPEARS IN
RELATED QUESTIONS
In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D.
In the given figure, AP is the bisector of ∠A and CQ is the bisector of ∠C of parallelogram ABCD. 
Prove that APCQ is a parallelogram.
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
In the following figures, find the remaining angles of the parallelogram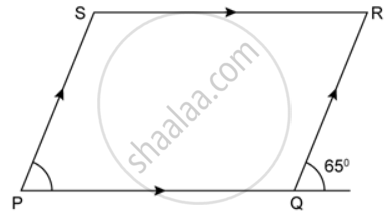
In the following figures, find the remaining angles of the parallelogram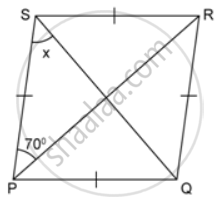
In the given figure, ABCD is a parallelogram, find the values of x and y.
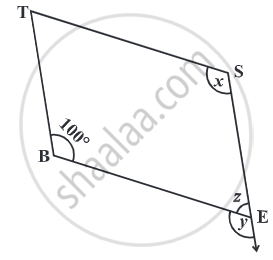
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
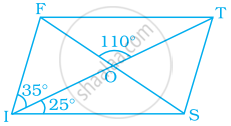
In parallelogram FIST, find ∠SFT, ∠OST and ∠STO.