Advertisements
Advertisements
Question
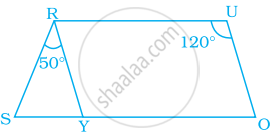
In the given parallelogram YOUR, ∠RUO = 120° and OY is extended to point S such that ∠SRY = 50°. Find ∠YSR.
Solution
Given, ∠RUO = 120° and ∠SRY = 50°
∠RYO = ∠RUO = 120° ...[∵ Opposite angles of a parallelogram]
Now, ∠SYR = 180° – ∠RYO ...[Linear pair]
= 180° – 120°
= 60°
In ΔSRY,
By the angle sum property of a triangle,
∠SRY + ∠RYS + ∠YSR = 180°
⇒ 50° + 60° + ∠YSR = 180°
⇒ ∠YSR = 180° – (50° + 60°)
⇒ ∠YSR = 180° – 110°
∴ ∠YSR = 70°
APPEARS IN
RELATED QUESTIONS
In the given figure, AP is the bisector of ∠A and CQ is the bisector of ∠C of parallelogram ABCD. 
Prove that APCQ is a parallelogram.
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
In the following figures, find the remaining angles of the parallelogram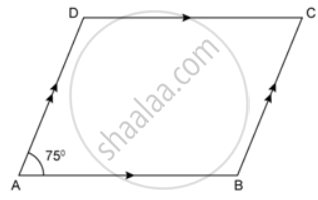
In the following figures, find the remaining angles of the parallelogram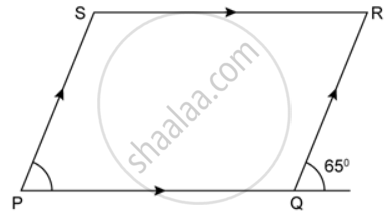
The consecutive angles of a parallelogram are in the ratio 3:6. Calculate the measures of all the angles of the parallelogram.
Find the measures of all the angles of the parallelogram shown in the figure: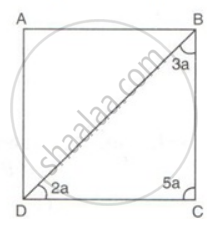
In the given figure, ABCD is a parallelogram, find the values of x and y.
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
PQR is a triangle formed by the adjacent sides PQ and QR and diagonal PR of a parallelogram PQRS. If in ΔPQR, ∠P : ∠Q : ∠R = 3 : 8 : 4, Calculate the measures of all the angles of parallelogram PQRS.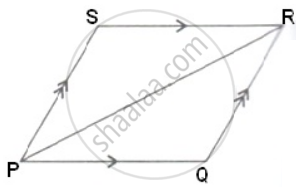
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
