Advertisements
Advertisements
Question
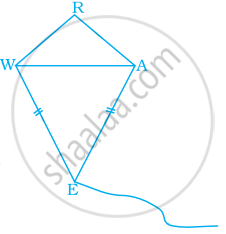
In kite WEAR, ∠WEA = 70° and ∠ARW = 80°. Find the remaining two angles.
Solution
Given, In a kite WEAR, ∠WEA = 70°, ∠ARW = 80°
Now, by the interior angle sum property of a quadrilateral,
∠RWE + ∠WEA + ∠EAR + ∠ARW = 360°
⇒ ∠RWE + 70 + ∠EAR + 80° = 360°
⇒ ∠RWE + EAR = 360° – 150°
⇒ ∠RWE + ∠EAR = 210° ...(i)
Now, ∠RWA = ∠RAW [∵ RW = RA] ...(ii)
And ∠AWE = ∠WAE [∵ WE = AE] ...(iii)
On adding equations (ii) and (iii), we get
∠RWA + ∠AWE = ∠RAW + ∠WAE
⇒ ∠RWE = ∠RAE
From equation (i),
2∠RWE = 210°
∠RWE = 105°
⇒ ∠RWE = ∠RAE = 105°
APPEARS IN
RELATED QUESTIONS
All rhombuses are kites.
Measures of opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of its each angle.
For which of the following, diagonals bisect each other?
Which of the following figures satisfy the following property?
- Has two pairs of congruent adjacent sides.
Which one has all the properties of a kite and a parallelogram?
A quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure is ______.
If only one diagonal of a quadrilateral bisects the other, then the quadrilateral is known as ______.
A kite is not a convex quadrilateral.
Every kite is a parallelogram.
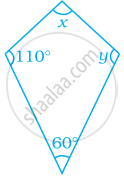
Find the values of x and y in the following kite.