Advertisements
Advertisements
Question
Prove that the bisectors of interior angles of a parallelogram form a rectangle.
Solution
Given:
ABCD is a parallelogram
AE bisects ∠BAD
BF bisects ∠ABC
CG bisects ∠BAD
DH bisects ∠ADC
To prove: LKJI is a rectangle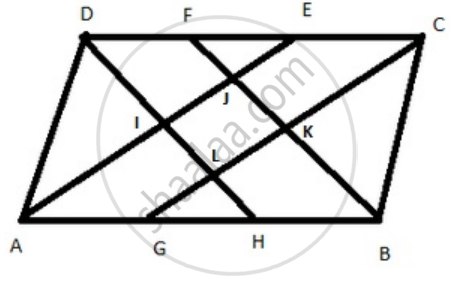
Proof :
∠BAD + ∠ABC = 180° ...[ adjacent angles of a parallelogram are supplementary ]
∠BAJ = `1/2` ∠BAD ...[AE bisects BAD ]
∠ABJ = `1/2` ∠ABC ... [DH bisect ABC ]
∠BAJ + ∠ABJ = 90° ...[ halves of supplementary angles are complementary ]
ΔABJ is a right triangle because its acute interior angles are complementary.
Similarly
∠DLC = 90°
∠AID = 90°
Then ∠JIL = 90° because ∠AID and ∠JIL are vertical angles
since 3 angles of a quadrilateral, LKJI are right angles, si is the 4th one and so is LKJI a rectangle, since its interior angles are all right angles
Hence proved.
APPEARS IN
RELATED QUESTIONS
The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
The diagonals PR and QS of a quadrilateral PQRS are perpendicular to each other. A, B, C and D are mid-point of PQ, QR, RS and SP respectively. Prove that ABCD is a rectangle.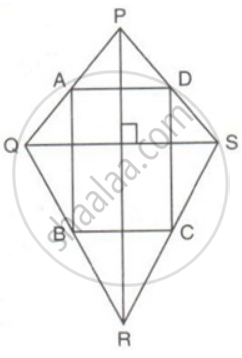
PQRS is a parallelogram. M and N are the mid-points of the adjacent sides QR and RS. O is the mid-point of the diagonal PR. Prove that MONR is a rectangle and MN is half of PR.
ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: areaΔAOD + areaΔBOC + areaΔABO + areaΔCDO.
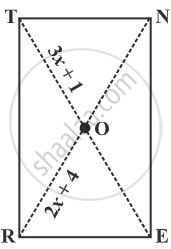
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is ______.
Diagonals of a rectangle are ______.
If one diagonal of a rectangle is 6 cm long, length of the other diagonal is ______.
Diagonals of a rectangle are equal.
Diagonals of rectangle bisect each other at right angles.
