Advertisements
Advertisements
Question
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Solution
Given: In quadrilateral ABCD, ∠A + ∠D = 180º.
We know that the sum of the two consecutive angle is 180º.
So, pair of opposite side AB and CD are parallel.
Since, the quadrilateral ABCD is trapezium.
Hence, special name can be given to this quadrilateral is trapezium.
APPEARS IN
RELATED QUESTIONS
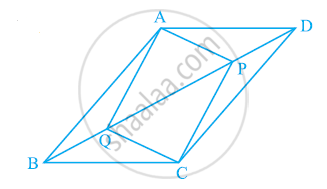
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
State, 'true' or 'false'
Every rhombus is a parallelogram.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.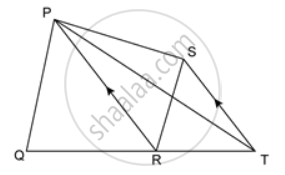
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.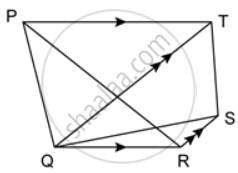
*Question modified
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Find the area of each of the following figure: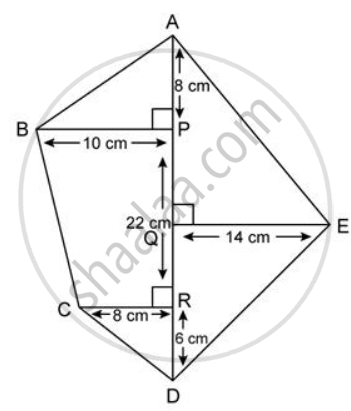
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Give reason for the following :
A square can be thought of as a special rectangle.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
