Advertisements
Advertisements
प्रश्न
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
उत्तर
Let the breadth of the rectangle = xm
The area of a rectangle with length l and breadth b = A = l x b
∴ The area of a rectangle with length 240m and breadth xm = A = 240x
⇒ 240x = 36000
⇒ x = `(36000)/(240)`
= 150m
Now, the perimeter of a rectangle with length l and breadth b = P = 2(l + b)
∴ The perimeter of a rectangle with length 240 and breadth 150 is
P = 2(240 + 150)
= 2(390)
= 780
The cost of fencing 1m = Rs.2.50
⇒ The cost of fencing 780m
= Rs.2.50 x 780
= Rs.1950.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.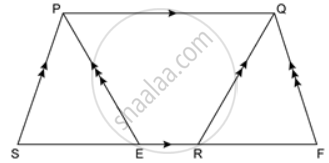
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reasons for the following :
A square can be thought of as a special rhombus.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
